循环流化床锅炉煤泥燃烧行为模型
煤泥泛指煤粉含水形成的半固体物,是煤炭生产过程中的一种副产品,其堆积形态极不稳定,作为废料废弃,易造成环境污染。同时煤泥具有高持水性、高灰分、低热值的特点,不宜进行复杂处理,采用输送燃烧是一种可靠的规模化处理煤泥的手段。循环流化床(CFB)锅炉具有良好的燃料适应性,是燃烧煤泥的一种有效方式,其相关问题已有学者进行了研究。
当前,采用输送方式的燃煤泥CFB锅炉的给料方式主要有:①炉顶泵送或刮板式给料;②中部喷射或泵送给料;③底部密相区泵送喷射给料。煤泥给料过程中,为保证输送管道不堵塞,通常在保证泵压下采用较大的管道直径。给料进入的煤泥形成较大的煤泥团,到达炉膛底部时,可能会影响床层的稳定性。此外,煤泥颗粒在炉膛内部受热,其表面首先被干燥,如干燥表层在下落过程中被磨损,形成的微小颗粒扬析进入飞灰,会影响燃煤泥CFB锅炉燃烧效率。因此,需要深入研究煤泥在炉膛内部的下落过程。
当前,已有学者研究了高水分低品质燃料,如水煤浆和泥煤的干燥和燃烧过程:Levi-Hevroni及A.Levy构建了湿颗粒和水煤浆的气力输送条件下的运动和干燥过程的一维模型,并与实验结果进行了对比;Agrawal等研究了流化床中颗粒的干燥过程;Omar等研究了不同粒径泥煤在流化床密相区燃烧不同阶段的温度变化;KijoKleczkowska等研究了流化床中不同煤种的水煤浆悬浊液的燃烧特性。但目前,干燥与燃烧模型建立与验证过程一般针对于微米级和毫米级的小粒径物料,其与给入CFB炉膛内部的煤泥颗粒的粒径条件和运动特性明显不同。同时,需要结合CFB锅炉炉膛内部床料分布特性分析煤泥在炉膛内部的运动和传热传质过程,而当前对于该问题的研究仍然较少。1模型的建立煤泥在CFB锅炉炉膛内的物理过程可以描述为:煤泥给入后,下落过程受到气体的曳力、床料的作用和重力的影响,在炉膛内部干燥、脱挥发分并燃烧。干燥过程中,颗粒内部的水分不足以补充蒸发的消耗,蒸发可能在内部发生。颗粒表层逐渐形成水分较低的干区,内部形成水分较高的湿区,如图1所示,图中rv为蒸发界面半径,Rp为颗粒半径。随干燥的进行,蒸发界面逐渐内移直至干燥完全并进入随后阶段。

针对该物理过程,对煤泥在CFB锅炉炉膛内运动和干燥过程做以下假设:(1)运动过程采用一维简化,炉膛内部的气固两相混合物简化为下部密度较高、上部密度较低的气固混合物。颗粒在其中受到床料颗粒相与煤泥颗粒的浮力、曳力和重力,沿高度方向构建一维模型;(2)煤泥结构简化为由惰性介质和水组成的球体,满足各向同性条件,若惰性介质与水密度近似相同,则惰性介质的孔隙率近似等于煤泥含水率。在干燥过程中,煤泥形状不发生变化;(3)颗粒内部不同物质(液态水、水蒸气、烟气、固相介质)在同一个位置达到热平衡,即同一个位置,具有相同的温度;(4)干燥过程中,干区只存在水蒸气、烟气和惰性介质;湿区只存在水分和惰性介质,水分呈自由态并均匀分布;干湿区界面为蒸发界面,其生成水蒸气并不断内移;(5)干燥过程中,干区压力与外界压力相同;(6)炉膛内部温度不变,外界向颗粒的传热过程是水分蒸发过程的惟一热源。
1.1 运动方程通过物理过程假设,建立煤泥的运动方程为

式中,u为流化风速;uP为颗粒速度;ρb为气固两相流的密度;ρP为煤泥颗粒密度;τ为时间;FD为颗粒的阻力项系数,其形式为
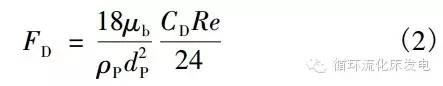
式中,u为流化风速;uP为颗粒速度;ρb为气固两相流的密度;ρP为煤泥颗粒密度;τ为时间;FD为颗粒的阻力项系数,其形式为

床料密度按2600kg/m3考虑,由实验确定炉膛内部不同高度的空隙率,亦即炉膛不同高度位置上气固混合物的密度,结果如图2所示。
1.2 湿区传热传质方程蒸发界面开始温度逐渐升高至100℃,蒸发由扩散控制,蒸发速率m″v为

1.2 湿区传热传质方程蒸发界面开始温度逐渐升高至100℃,蒸发由扩散控制,蒸发速率m″v为
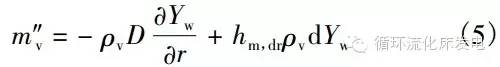
式中,ρv为蒸发界面的水蒸气密度;r为颗粒当地半径;hm,dr为蒸发界面对流传质系数;Yw为水蒸气质量分数;D为水蒸气的扩散系数。蒸发界面温度上升至100℃后,热量均用以相变蒸发,传热量q″v为

式中,λv为水蒸气导热系数;hdr为蒸发界面对流换热系数;t为颗粒当地温度。蒸发速率m″v为

式中,hf-g为水的蒸发潜热。考虑颗粒孔隙率εp,蒸发界面迁移速度为

式中,ρw为水的密度。由能量守恒方程得到湿区内部的传热方程为
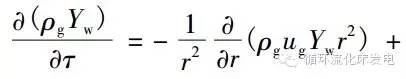
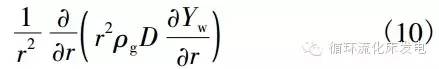
式中,ρg为颗粒内烟气相密度;对流项速度ug由等压假定得到

则式(10)简化为


式中,cpv为水蒸气的比热容;cpf为干烟气的比热容;cpc为煤干基的比热容。
1.4 颗粒表面的边界条件颗粒表面与外界发生对流和辐射换热,根据工程上的处理方式,总换热系数h为对流换热系数hc和辐射换热系数h之和。颗粒与外界的对流换热系数考虑床层空隙率εb的影响,有

表面对流换热系数hc为

式中,λ为烟气的导热系数。表面辐射换热系数hr为

式中,ε为颗粒与床层间的表观发射系数;σ为斯忒潘-玻尔兹曼常数;Tp为颗粒外表面绝对温度;Tb为床层绝对温度。
1.5 离散化及工况的计算
计算过程逐次求解运动和传热传质方程。温度T和质量分数Yw采用Crank-Nicolson隐式差分格式,以保证方程稳定域。小室数量选取考虑网格无关性,保证颗粒表层单元温度与网格精度无关。
计算选取1~500mm颗粒和3~5m/s流化风速,具体工况根据煤泥和锅炉参数确定。初始高度为距布风板15,35,55m;炉温为900℃;初始水分含量为33%。颗粒粒径和流化风速对运动影响计算如图3所示1mm小颗粒被携带向上运动。顶部给料时,顶部流体速度实际不能简单视为与底部相同,小颗粒首先下落,随后被反向携带,在炉膛内干燥并燃烧。10mm颗粒开始受到的曳力与浮力之和小于重力,颗粒加速运动。随着运动速度增加,其受到的曳力逐渐增大,速度达到稳定。靠近下方床层后,其受到床料颗粒的作用逐渐增大,速度逐渐减小,最终稳定在某一高度燃烧。100,500mm颗粒开始时加速下落,到达最大值之后,在靠近床层附近速度大幅下降,最终到达床层达到稳定。
进一步以颗粒速度小于0.1m/s或到达布风板上方2m作为稳定条件,计算不同粒径颗粒的稳定时间(表1)。
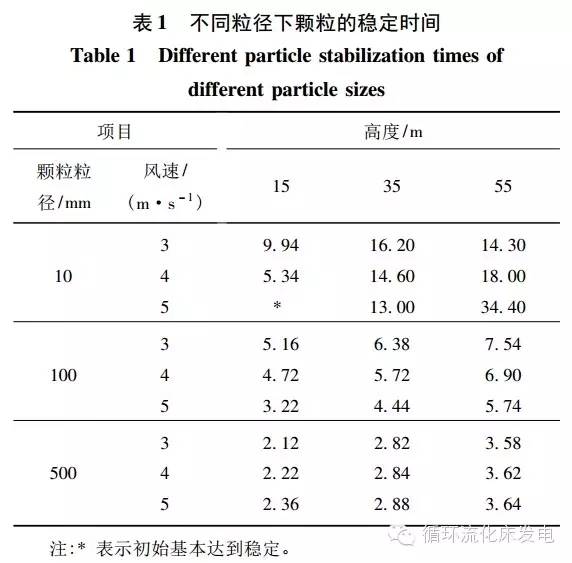
为清晰体现出粒径对颗粒运动行为的影响,选取10,100,500mm作为特征粒径。结合图3分析,给料高度和风速对大颗粒的稳定时间影响较小。

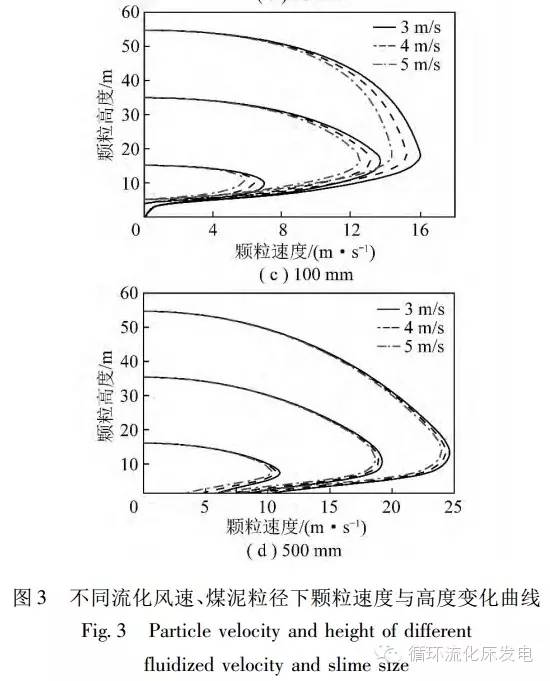
10mm颗粒中部和底部与顶部给料时风速对稳定时间的影响趋势不同。中部和底部给料时,颗粒到达最大速度后很快进入减速阶段,影响因素主要为颗粒的减速过程,高风速造成了较大的曳力,使煤泥颗粒较快达到稳定。顶部给料时,影响因素主要为颗粒在稀相区的稳定速度,较低的流化风速使颗粒较快到达床层附近进入减速阶段。
结合表1和图3,得到不同风速下颗粒达到稳定的粒径转变点在100mm左右,因此有必要在100mm附近进行详细计算。顶部给料时30~300mm颗粒的稳定时间计算结果如图4所示。

顶部给料时,随粒径增大,颗粒稳定时间在下降过程中出现峰值。随流化风速增大,峰值后移,同时峰高降低。
较小颗粒给入炉膛内部后,煤泥颗粒最终悬浮,稳定时间取决于颗粒的运动与减速过程。随粒径增大,颗粒在上部稀相的终端速度增加,到达底部时间

4m/s流化风速下,200mm颗粒到达床层前速度快速下降,到达床层的速度为1~2m/s,基本不会影响床层稳定。300mm颗粒到达床层速度为3~8m/s;500mm颗粒到达床层速度为7~14m/s。一般认为,团聚物料接触床层绝对速度不超过6.5m/s时,可保证床层稳定。因此,300~500mm颗粒在运行中需要加以关注。
为分析颗粒在炉膛内部干燥情况,计算了4m/s流化风速下,100,500mm颗粒落至距布风板上方5m时的表层温度分布,如图5所示。

100,500mm颗粒到达床层底部前,均未完全干燥。500mm颗粒到达底部床层时间较短,同时颗粒粒径较大,较100mm颗粒干燥程度低。颗粒表层与内部之间温度具有明显差异。顶部给入的100mm颗粒,最终表层温度为292℃,而内部仍未干燥。
定义蒸发界面与颗粒表面之间的距离(即干区厚度)为干燥层厚度,得到顶部给料时100mm颗粒的干燥层厚度为0.54mm,体积分数为3.24%;底部给料时的干燥层厚度为0.25mm,体积分数为1.5%。500mm颗粒顶部给料时,干燥层厚度为0.36mm,体积分数为0.43%。若忽略干燥层剥落对干燥过程的影响,并假定干燥层全部剥落,且因颗粒太细而一次通过炉膛,导致燃烧效率较低。由于下落过程中可剥落干燥层仅占整体的很小部分,对燃烧效率不会有较大影响。但颗粒越小,其对燃烧效率造成影响的可能性越大。因此,实际运行的给料粒径同样不宜过小。
表3为大颗粒落至布风板上方5m时的表层温度。随颗粒增大,到达底部的干燥表层温度降低,300,500mm颗粒到达床层时,表层温度为200℃左右。
(1)煤泥颗粒运动性质与其粒径相关,较小颗粒下降达到某一位置之后稳定燃烧;较大颗粒首先加速运动,随后受到床层上方颗粒的阻力作用,速度迅速下降,最终落到床层表面。随粒径增大,颗粒的稳定时间整体减小,但其存在一个先上升后下降的峰值,其位置与高度与颗粒稳定形式相关。
(2)200mm的颗粒在不同位置给入时,其在床层上方速度快速下降,最终为1~2m/s,对于床层影响不大。随颗粒粒径增大,颗粒对于床层的影响增大。顶部给料时,需要注意300~500mm颗粒对于床层的影响。
(3)能够到达底部的大颗粒,其干燥层相对很小,对于整体燃烧效率影响较小。随颗粒粒径的增大,其到达底部的时间缩短而需要加热的颗粒增大,其干燥层减小。到达底部的颗粒表面与内部的温差较大。
尹炜迪,李博,吴玉新,杨海瑞,刘青,吕俊复,赵锦洋. 循环流化床锅炉煤泥燃烧行为模型[J]. 煤炭学报,2015,v.40;No.25007:1628-1633.
